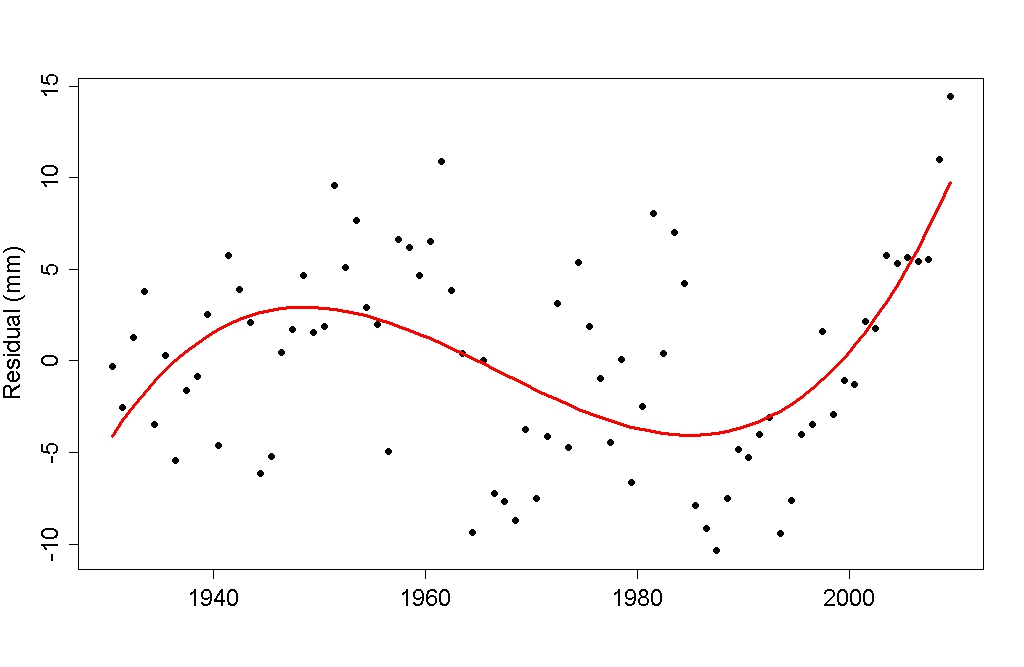
21. Text: Higher Order Terms

How to Identify Higher Order Terms?

Higher order terms in linear models are created when multiplying two or more x-variables by one another. Common higher order terms include quadratics (x_1^2) and cubics (x_1^3) , where an x-variable is multiplied by itself, as well as interactions (x_1x_2) , where two or more x-variables are multiplied by one another.

In a model with no higher order terms, you might have an equation like:

\hat{y} = b_0 + b_1x_1 + b_2x_2

Then we might decide the linear model can be improved with higher order terms. The equation might change to:

\hat{y} = b_0 + b_1x_1 + b_2x_1^2 +b_3x_2 + b_4x_1x_2

Here, we have introduced a quadratic (b_2x_1^2) and an interaction (b_4x_1x_2) term into the model.

In general, these terms can help you fit more complex relationships in your data. However, they also take away from the ease of interpreting coefficients, as we have seen so far. You might be wondering: "How do I identify if I need one of these higher order terms?"

When creating models with quadratic, cubic, or even higher orders of a variable, we are essentially looking at how many curves there are in the relationship between the explanatory and response variables.

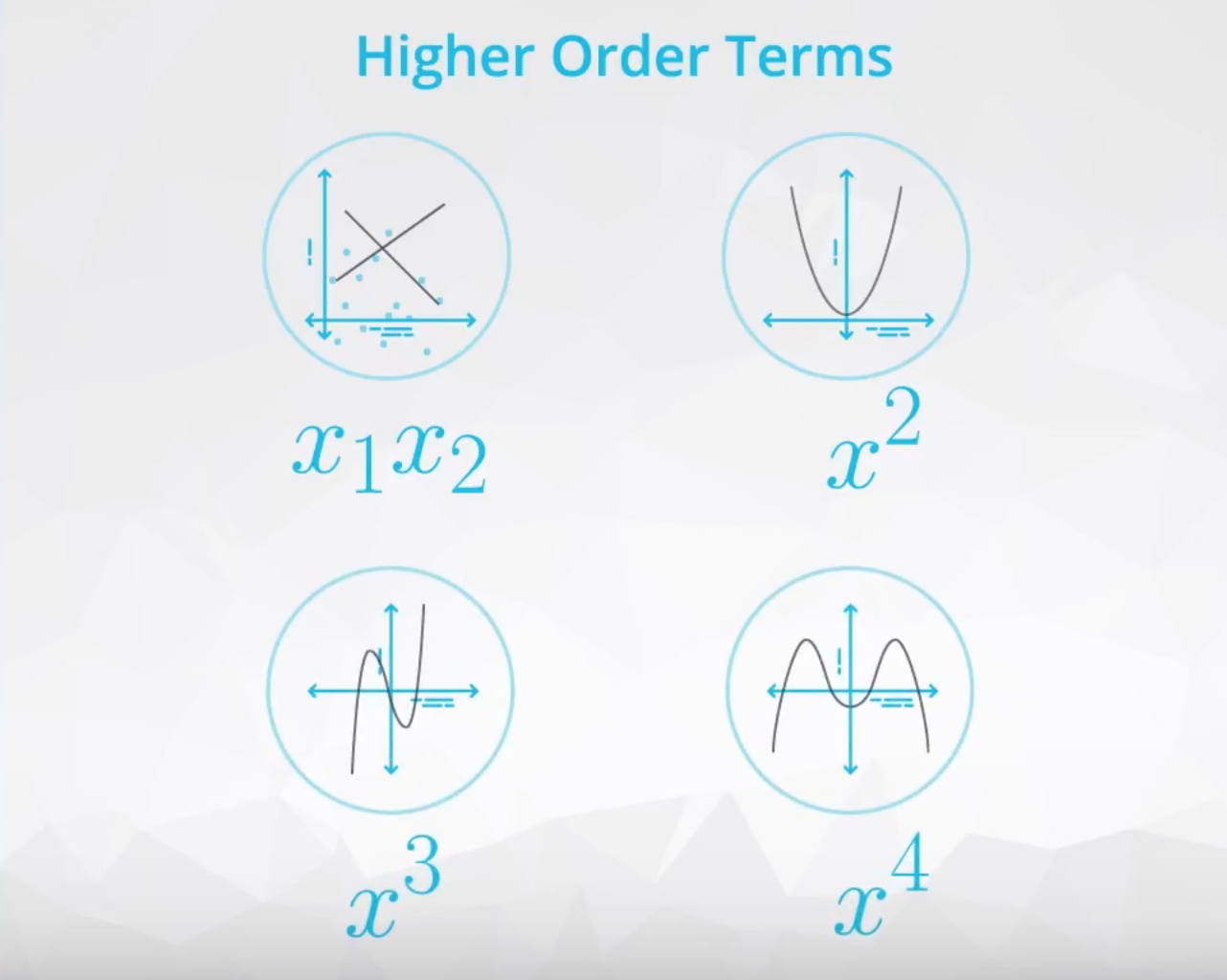
If there is one curve, like in the plot below, then you will want to add a quadratic. Clearly, we can see a line isn't the best fit for this relationship.

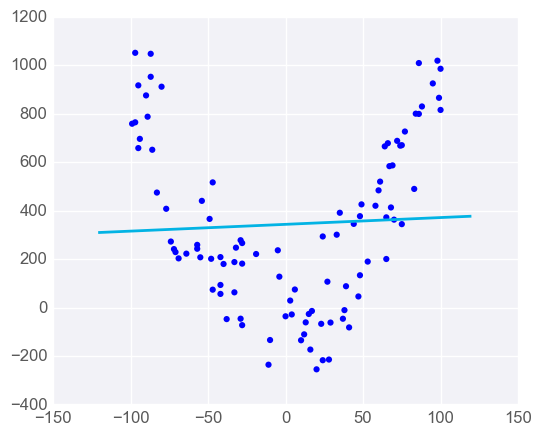
Then, if we want to add a cubic relationship, it is because we see two curves in the relationship between the explanatory and response variable. An example of this is shown in the plot below.

Diving into these relationships a little more closely and creating them in your linear models in Python will be the focus in the upcoming videos.